개요

두 문자열의 가장 긴 공통 부분문자열을 찾는 Longest Common Subsequence (LCS) 문제는 정보과학에서 기초가 되는 잘 알려진 문제이다. 이렇게 기초적임에도 불구하고, LCS 문제는 생물정보학이나 전산언어학, 그리고 실생활에서 자주 사용하는 검색 엔진 등 다양한 학문과 분야에서 활용되는 아주 중요한 문제이다.

길이가 각각 $L_1, \cdots, L_N$인 문자열 $N$개의 LCS는 다이나믹 프로그래밍 기법을 이용하여 $\displaystyle \mathcal{O} \left( N \prod _{k=1}^{N} L _k \right) $의 시간 복잡도로 해결할 수 있음이 잘 알려져 있다.

본 글은 길이 $N$, $M$ $(N \gg M)$의 두 문자열의 LCS를 평균 $\displaystyle \mathcal{O} \left( N \lg N \right)$에 해결하는 효율적인 알고리즘을 소개하고 그 응용 방안에 대하여 알아본다.

본문에서는 다음의 내용을 부가적인 설명 없이 서술한다. 각 항목에 대하여, 자세하게 서술한 좋은 글을 링크해두었다.

문제 제기

가장 긴 공통 부분문자열 문제

어떤 문자열 $S$의 부분문자열 (Subsequence)의 정의는 다음과 같다.

문자열 $S = s _1 s _2 \cdots s _N$의 부분문자열 $s _{i _1} s _{i _2} \cdots s _{i _K}$은 정수열 $\left\{ i _k \right\} _{k = 1}^{k = K}$로 생성되는 문자열이다. 여기서 수열 $\left\{ i _k \right\} _{k = 1}^{k = K}$는 다음 조건을 만족해야 한다.

$0 \le K \le N$

$\displaystyle 1 \le i _1 < i _2 < \cdots < i _K \le N$

즉, 부분문자열은 원 문자열에서 순서를 유지한 채 몇 개의 문자를 제거하여 얻어질 수 있는 문자열을 뜻한다.

가장 긴 공통 부분문자열 (LCS) 문제란, $K$개의 문자열이 주어질 때, 모든 문자열의 공통 부분문자열 중에서 최장인 것을 찾는 문제이다. 이러한 문제는 특히 생물정보학에서 자주 사용되며, 단백질의 아미노산 서열이나, DNA, RNA의 염기 서열의 LCS를 계산하여 얼마나 그 구조가 유사한지를 분석하는 데에 응용될 수 있다.

1978년에 David Maier는 문자열의 개수 $K$를 변수로 두면, LCS 문제는 NP-Hard가 됨을 증명하였다. 본 글에서는 $\displaystyle K = \mathcal{O} \left( 1 \right) $, 특히 $K = 2$로 가정한다.

고전적인 DP 알고리즘

LCS 문제는 동적 계획법 (Dynamic Programming)을 이용하여 쉽게 해결할 수 있다.

먼저, 두 문자열 $X$, $Y$에 대하여, $\text{LCS} (X, Y)$를 “$X$와 $Y$의 최장 공통 부분문자열의 집합”으로 정의하자.

Lemma 1. 공통 접미사는 LCS에 포함된다.

임의의 문자열 $X$, $Y$, $S$에 대하여, 다음이 성립한다.
\[\text{LCS} \left( X + S, Y + S \right) = \text{LCS} \left( X, Y \right) + S := \left\{ C + S : C \in \text{LCS} \left( X, Y \right) \right\}\]

이는 $\left\lvert S \right\rvert = 1$일 때에만 증명해도 충분하다. $X + S$와 $Y + S$의 마지막 문자는 서로에게 대응시키는 것이 LCS를 구함에 있어 손해가 되지 않기 때문에 항상 최적임을 알 수 있다.

Lemma 2. 양자택일.

임의의 문자열 $X$, $Y$와 서로 다른 두 알파벳 $\alpha, \beta \in \Sigma$에 대하여, 다음이 성립한다.
\[\text{LCS} \left( X + \alpha, Y + \beta \right) = \max \left[ \text{LCS} \left( X + \alpha, Y \right), \text{LCS} \left( X, Y + \beta \right) \right]\]
여기서, $ \max \left[ U, V \right] $는 $U \cup V$에서 길이가 가장 긴 문자열만 모아놓은 문자열 집합을 의미한다.

$\alpha \ne \beta$이므로, 두 알파벳은 서로에게 대응될 수 없다. 즉, 둘 중 하나는 공통 부분문자열에 포함되지 못하므로, 각각의 경우에 대하여 LCS를 계산한 후 합쳐줄 수 있다. $\alpha = \beta$인 경우는 Lemma 1.에 해당함에 유의하라.

우리는 이 두 Lemma를 적용하여 LCS의 길이를 계산할 수 있다.

두 문자열 $X = x _1 x _2 \cdots x _N$, $Y = y _1 y _2 \cdots y _M$에 대하여, $D _{i, j}$를 $X[1 \cdots i]$와 $Y[1 \cdots j]$의 LCS 길이로 정의하자. 그러면 다음과 같은 재귀적 관계식을 세울 수 있다.

$x _i = y _j$라면, $ D _{i, j} = D _{i-1, j-1} + 1 $

그렇지 않다면, $ D _{i, j} = \max \left\{ D _{i, j-1}, D _{i-1, j} \right\} $

전자는 Lemma 1., 후자는 Lemma 2.에 대응됨에 유의하라.

따라서, 두 문자열의 LCS의 길이는 $D _{N, M}$과 같고, 이 값은 $\displaystyle \mathcal{O} \left( NM \right)$의 시간 복잡도로 계산할 수 있다. $\text{LCS}(X, Y)$ 중 하나의 원소를 알아내는 작업은 $D _{N, M}$의 값이 어디로부터 왔는지를 역추적하여 계산할 수 있다.

이를 코드로 구현하면 다음과 같다.

// input: two strings X[0 ... N-1], Y[0 ... M-1]
// output: length of LCS(X, Y)
int lcs(char *X, int N, char *Y, int M) {
    int D[N+1][M+1] = {}; // D_{i, j}
    
    for(int i = 1; i <= N; i++)
        for(int j = 1; j <= M; j++)
            D[i][j] = X[i] == Y[j]
                    ? D[i-1][j-1] + 1 // Lemma 1.
                    : max(D[i][j-1], D[i-1][j]); // Lemma 2.
    
    return D[N][M];
}

Hunt-Szymanski Algorithm

더 빠른 알고리즘의 필요성 제기

해싱이나 문자의 값을 사용하지 않고, 두 문자열의 LCS를 알아내기 위해서는 $\mathcal{O} \left( NM \right)$번의 문자쌍 비교가 반드시 필요함이 D S. Hirschberg와 J D. Ullman에 의하여 1974년에 증명되었다. 즉, 상기한 고전적 DP 알고리즘은 LCS를 계산하는 최적의 알고리즘이다.

그러나 현실에서, 그리고 많은 정보과학 관련 학문 분야에서 LCS 문제는 자주 사용되기에, 아주 긴 문자열의 LCS를 빠르게 계산하는 알고리즘의 필요성이 점차 대두되었다.

1970년대에 개발된 Hunt-Szymanski 알고리즘은 간단한 아이디어로 두 문자열의 LCS를 $\displaystyle \mathcal{O} \left( N \lg N \right)$의 실험적 시간 복잡도로 계산한다. 본 글은 이 알고리즘의 아이디어와 구현 방법을 소개하고자 한다.

핵심적 관찰

먼저, 고전적 DP 알고리즘의 작동 방식을 생각하자.

두 문자열 aeaca와 acea에서 같은 알파벳을 가지는 모든 위치쌍을 ‘X’표로 나타내면 아래와 같다.

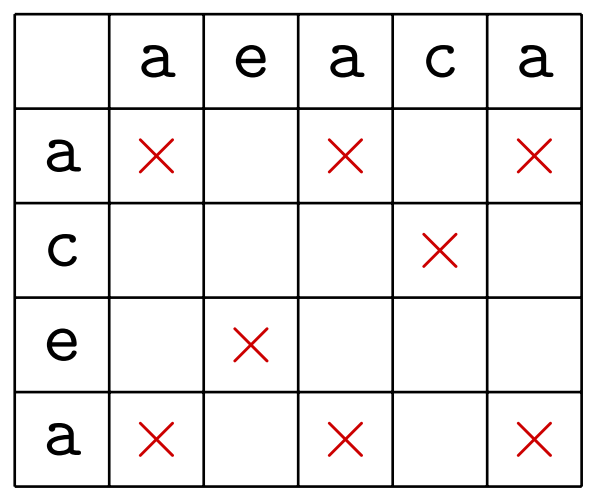
그림 1: 두 문자열의 공통 알파벳에 대응되는 모든 위치를 표시한 표

두 문자열 $X$, $Y$에 대하여, $x _i = y _j$인 모든 위치쌍 $(i, j)$을 'X'표로 나타내었다.

고전적 DP 알고리즘은 $D _{i, j}$의 값을 구할 때 일반적으로 $D _{i, j-1}$과 $D _{i-1, j}$의 최댓값을 채택하나, ‘X’표에 해당하는 위치에서만 $D _{i-1, j-1} + 1$의 값을 택하는 알고리즘이다.

그러나, 실생활에서, 알파벳의 총 개수가 충분히 크다면, 이러한 ‘X’표의 개수가 $\displaystyle \mathcal{O} \left( NM \right) $보다는 유의미하게 작으리라 기대할 수 있다. Hunt-Syzmanski 알고리즘은 이러한 아이디어에서 출발한다.

Lemma 3. $D _{, }$의 행의 단조성

고전적 DP 알고리즘에서 한 행 $D _{i, *}$의 값은 항상 다음과 같은 형식을 가진다.
\[0\ 0\ 1\ 1\ 1\ 2\ 3\ 3\ 3\ 3\ 3\ 4\ 4\ 5\ 5\ 5\ \cdots\]
즉, 첫 번째 값은 항상 0이고, 이웃한 두 수의 차이는 최대 1이며, 값을 차례대로 읽으면 단조증가한다.

단, 편의상 $D _{0, * } = D _{ *, 0} = 0$라고 가정한다.

행 번호 $i$에 대하여 귀납법을 적용하여 증명할 수 있다. $D _{0, *}$은 그 값이 모두 0이므로 자명하다. $D _{i, j}$의 값은 (1) 그 이전 값 $D _{i, j-1}$거나, (2) 그 위의 값 $D _{i-1, j}$거나, (3) 대각 위의 값 $D _{i-1, j-1}$에서 1을 더한 값이다. 인접한 수의 차이는 0 아니면 1이므로, $D _{i, *}$ 또한 단조증가하면서 차이가 최대 1인 수열임을 알 수 있다.

이제, 각 행에 대하여 연속한 값을 가지는 구간의 특징을 관찰하자. 같은 값을 가지는 Segment에서 첫 수를 Head, 나머지 수들을 Tail이라고 부르자. 어떤 행의 $D _{i, *}$ 값이 $ 0\ 0\ 0\ 0\ 0\ 1\ 1\ 1\ 1\ 2\ 3\ 3\ 3\ 3\ 4\ 4\ 4\ 4 $일 때, 각 Segment의 Tail을 직사각형 블록으로 묶어서 표현하면 아래와 같다.

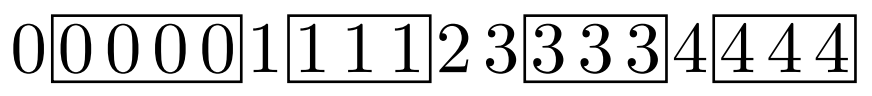
그림 2: 한 행에서 모든 Tail을 직사각형으로 나타낸 그림

총 네 개의 Tail을 직사각형으로 묶어 나타내었다. Head의 값이 차례대로 0, 1, 2, 3, 4 임에 유의하라.

그림 2와 같이 $D _{i, *}$ 값을 Segment 표기법으로 나타낸 후, 그 바로 아래의 행에서 ‘X’표 배치에 따른 $D _{i+1, *}$ 값 변화를 관찰하자. 만약, 그림 3의 상단과 같이 ‘X’표가 배치되었다면, $D _{i+1, *}$의 값은 하단과 같이 결정된다.

그림 3: 'X'표 배치와 그 아래 행의 값

그림 2의 $D _{i, *}$과 'X'표 배치가 상단과 같이 주어지면, $D _{i+1, *}$의 값은 하단과 같이 결정된다.

여기서 우리는 다음의 사실을 관찰할 수 있다.

Theorem.

Head 아래에 있는 ‘X’표는 무시해도 $D _{i+1, *}$ 값에 변화를 주지 않는다.

같은 Tail에 여러 개의 ‘X’표가 있다면, 가장 앞에 있는 ‘X’표만 남겨도 그 결과는 동일하다.

각 Tail의 가장 앞에 있는 ‘X’표는 $D _{i+1, *}$의 값을 1 증가시킨다.

알고리즘의 구현

$D _{*, 0} = 0$이고 값이 증가한다면 증감량이 무조건 1이므로, 각 행에서 $D _{i, *}$ 값이 증가하는 시점만 기록해도 모든 정보를 나타내기에 충분하다.

조금 더 자세하게는, $D _{i, j} - D _{i, j-1} = 1$인 $j$만 모아놓은 집합 $S _i$는 $D _{i, *}$의 모든 값을 잘 표현한다. 뿐만 아니라, $D _{i, *}$는 $\Theta \left( M \right)$의 공간 복잡도가 필요한 반면, $\left\lvert S _i \right\rvert$는 $M$보다 충분히 작을 것이라 기대할 수 있다. 실제로 이 집합의 크기가 어느 정도인 지는 추후에 분석한다.

예를 들어, 그림 3에서 $D _{i, *}$과 $D _{i+1, *}$의 값으로부터 집합 $S _i$, $S _{i+1}$을 계산하면 아래와 같다.

\[S _i = \left\{ 5, 9, 10, 14 \right\}\] \[S _{i+1} = \left\{ 2, 9, 10, 12, 16 \right\}\]

그러면, $S _i$와 ‘X’표 배치로부터 집합 $S _{i+1}$는 어떻게 얻을 수 있을까. 먼저, 다음과 같이 함수 $\text{succ}(S, x)$를 정의하자.

\[\text{succ} \left( S, x \right) := \min \left\{ y \in S : y \ge x \right\}\]

이 함수는 C++의 std::lower_bound에 대응된다.

$i+1$번째 행에 위치한 ‘X’표의 좌표를 모두 모아놓은 집합을 $R _i$라고 하자. 즉, $R _i := \left\{ j : x _{i+1} = y _j \right\}$이다. 이때, $S _{i+1}$는 다음과 같이 계산할 수 있다.

$S _{i+1} \longleftarrow S _i$ : 집합 $S _i$를 $S _{i+1}$에 복사한다.

각 $j \in R _i$를 감소하는 순서대로 다음을 반복한다.

$S _{i+1}$에서 $\text{succ} \left( S _{i+1}, j \right)$를 제거한다.

$S _{i+1}$에 $j$를 추가한다.

이러한 알고리즘의 정당성은 Theorem.에서 직관적으로 얻어진다.

이를 코드로 구현하면 다음과 같다. 고전적 DP 알고리즘과 비교하여도, 코드가 상당히 짧고 간결함을 알 수 있다.

// input: two strings X[0 ... N-1], Y[0 ... M-1]
// output: length of LCS(X, Y)
int lcs(char *X, int N, char *Y, int M) {
    vector<int> idx[256]; // # of alphabets = 256
    
    // Counting sort + Reverse
    // We use them to compute R_i fast
    for(int i = M; i--;) idx[Y[i]].emplace_back(i);
    
    // Init S_0
    int S[N+1] = {-1}, l = 1;
    
    // Compute S_1, ..., S_N
    for(int i = 0; i < N; i++) {
        for(int j : idx[A[i]]) {
            if(S[l-1] < j) S[l++] = j; // No succ. exists
            else S[int(lower_bound(S, S+l, j) - S)] = j;
                // Find succ. and replace
        }
    }
    
    return l-1;
}

결론

LCS 문제는 정보과학에서 기초적인 문제이지만, 생물정보학과 전산언어학, 검색 엔진, diff 프로그램 등, 학문적으로도 실용적으로도 다양한 분야에 접목되고 활용된다.

두 개의 문자열의 LCS를 구하는 문제는 해싱 등의 기법을 활용하지 않고서는 $\displaystyle \mathcal{O} \left( NM \right)$보다 빠르게 해결할 수 없음이 알려져 있다. 우리는 같은 알파벳을 나타내는 위치쌍의 총 개수 $\displaystyle R := \sum _i \left\lvert R _i \right\rvert$가 실험적으로는 $\displaystyle \mathcal{O} \left( NM \right)$보다는 유의미하게 작다는 사실을 활용한 Hunt-Szymanski 알고리즘에 대하여 알아보았다.

이 알고리즘은 고전적 DP 알고리즘에서 인접한 두 행의 $D _{i, *}$, $D _{i+1, *}$ 값의 특징을 관찰하고, 이 DP 배열을 적은 개수의 수로 이루어진 집합으로 표현함으로써, 평균 시간 복잡도를 낮추었다. $N \gg M$을 가정하면, 시간 복잡도는 $\displaystyle \mathcal{O} \left( R \lg N + M \lg M \right)$가 되며, $R = \Theta \left( NM \right)$인 최악의 경우에도 고전적 DP 알고리즘보다 $\displaystyle \mathcal{O}\left( \lg N \right)$배밖에 느리지 않다. 또한, 실험적으로는 $\displaystyle R = \mathcal{O} \left( N \right)$을 기대할 수 있다.

Hunt-Szymanski 알고리즘의 핵심적인 관찰들은 추후 Bit-String LCS 알고리즘에 응용되었다. 이 알고리즘은 $\displaystyle \mathcal{O} \left( \frac{ NM }{ \omega } \right)$의 시간 복잡도와 $\displaystyle \mathcal{O} \left( \frac{ \left\lvert \Sigma \right\rvert M }{ \omega } \right)$의 공간 복잡도로 LCS를 계산한다.

개요