개요

정수론에서 주로 다루는 중요한 수론적 함수로는 약수 함수 $\sigma_k (n)$, 오일러 피 함수 $\phi (n)$, 뫼비우스 함수 $\mu (n)$ 등이 있다. 이러한 함수의 학문적 중요도는 이루 말할 수 없으며, 컴퓨터과학와 PS 분야에도 종종 등장할 정도로 다양하게 활용된다.

본 글은 수론적 함수의 대표인 약수 함수 $\sigma (n)$의 구간 합을 효율적으로 계산하는 알고리즘을 서술한다. 함수의 합을 기하적으로 해석한 후, 이를 Stern-Brocot Tree 자료구조로 계산한다. 이후, 이 알고리즘의 시간 복잡도가 $\tilde{O} \left( N^{1/3} \right)$로 아주 효율적임을 보인다.

문제 제기

약수 함수의 합 문제

양의 정수 $n$에 대하여, $n$의 모든 양의 약수의 $k$제곱의 합을 생각하자. 이것이 약수 함수 $\sigma_k (n)$의 정의이다.

\[\sigma_k (n) := \sum_{ d | n } d^k\]

이 글에서는 $k = 1$인 시그마 함수 $\sigma (n) := \sigma_1 (n)$에 대하여 주로 다룬다. 이 값은 $n$의 약수의 합을 나타낸다.

이제, 정수 $N$이 주어졌을 때, 1부터 $N$까지 시그마 함숫값의 합 $ \displaystyle \sum_{k=1}^{N} \sigma(k) $을 구하는 문제를 생각하자.

정수론적 접근

$\sigma(1) + \cdots + \sigma(N)$의 값은 다음 조건을 만족하는 양의 정수 쌍 $(n, d)$의 개수와 같다.

$d$는 $n$의 약수

$1 \le d \le n \le N$

이는 시그마 함수의 정의를 생각할 때, $\sigma(k)$의 값은 $n = k$인 $(n, d)$의 개수와 같으므로 자명하다.

이제, $d$의 값을 고정한 후, 위의 조건을 만족하는 $n$의 개수를 세자. $n$은 $N$ 이하인 $d$의 배수라야 하므로, 총 $ \displaystyle \left\lfloor \frac{ N }{ d } \right\rfloor $개만큼 존재한다.

\[\sum _{k=1}^{N} \sigma(k) = \sum _{d=1}^{N} \left\lfloor \frac{ N }{ d } \right\rfloor\]

이는 다르게 해석하면, $y = \frac{N}{x}$ 그래프 아래에 있는 양의 정수 쌍 $(x, y)$의 개수를 세는 것과 같다. 곡선 $xy = N$은 직선 $x = y$에 대하여 대칭이며, 이 둘의 교점은 $\left( \sqrt{N}, \sqrt{N} \right)$이므로, 최종적으로 아래의 식을 얻을 수 있다.

\[\sum _{d=1}^{N} \left\lfloor \frac{ N }{ d } \right\rfloor = 2 \sum _{x=1}^{ \left\lfloor \sqrt{N} \right\rfloor } \left\lfloor \frac{ N }{ x } \right\rfloor - { \left\lfloor \sqrt{N} \right\rfloor }^2\]

우리는 시그마 함수 $\sigma(n)$의 값을 어떻게 계산하는지 알지 않아도, 시그마 함수의 합을 $O \left( \sqrt{N} \right)$만에 쉽게 계산할 수 있게 되었다.

그러나 $N$이 $10^{18}$-scale로 아주 큰 수라면, 우리는 이보다도 더욱 효율적인 방법을 찾아야 한다.

Stern-Brocot Tree

효율적인 알고리즘을 구상하기 전에, 페리 수열과 Stern-Brocot Tree 자료구조에 대하여 먼저 알아보자.

Farey Sequence

Stern-Brocot Tree에 대하여 논하기 전에, 먼저 페리 수열의 정의를 소개한다. $n$번째 페리 수열 $F_n$는 다음을 만족하는 모든 기약분수 $ \displaystyle \frac{a}{b} $를 오름차순으로 나열한 수열이다.

$0 \le b \le a \le n$

$\gcd (a, b) = 1$

예를 들어, 몇몇의 $n$에 대하여 페리 수열 $F_n$을 나열하면 아래와 같다.

\[F _1 = \left\{ \frac{0}{1}, \frac{1}{1} \right\}\] \[F _2 = \left\{ \frac{0}{1}, \frac{1}{2}, \frac{1}{1} \right\}\] \[F _5 = \left\{ \frac{0}{1}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{1}{1} \right\}\]

여기서, 페리 수열 $F_n$에서 인접한 두 유리수를 “차수 $n$에서 페리 이웃하다”라고 한다. 페리 이웃에 관한 중요한 정리를 하나 소개한다.

차수에 상관없이, 페리 이웃한 두 유리수 $ \displaystyle \frac{a}{b} > \frac{c}{d} $는 $ad - bc = 1$을 만족한다.

이 정리는 아래에 서술할 Stern-Brocot Tree에 관한 정리의 기반이 된다.

Stern-Brocot Tree

페리 수열 $F_n$을 확장하여, 각 유리수의 역수까지 등장하는 수열을 생각하자. 편의상, $ \displaystyle \frac{1}{0} = + \infty $로 생각하면, 이 수열은 $ \displaystyle \frac{0}{1} = 0 $ 이상 $ \displaystyle \frac{1}{0} = + \infty $ 이하인 기약분수를 잘 나열할 것이다.

실제로, $0$ 이상의 모든 유리수는 충분히 큰 $n$에 대하여 확장된 페리 수열 $F’ _n$에 정확하게 한 번 등장함을 증명할 수 있다. 이제, 깊이 $n$에 해당하는 층에 확장된 페리 수열 $F’ _n$을 적어, 아래 그림과 같은 이진 트리를 생각하자.

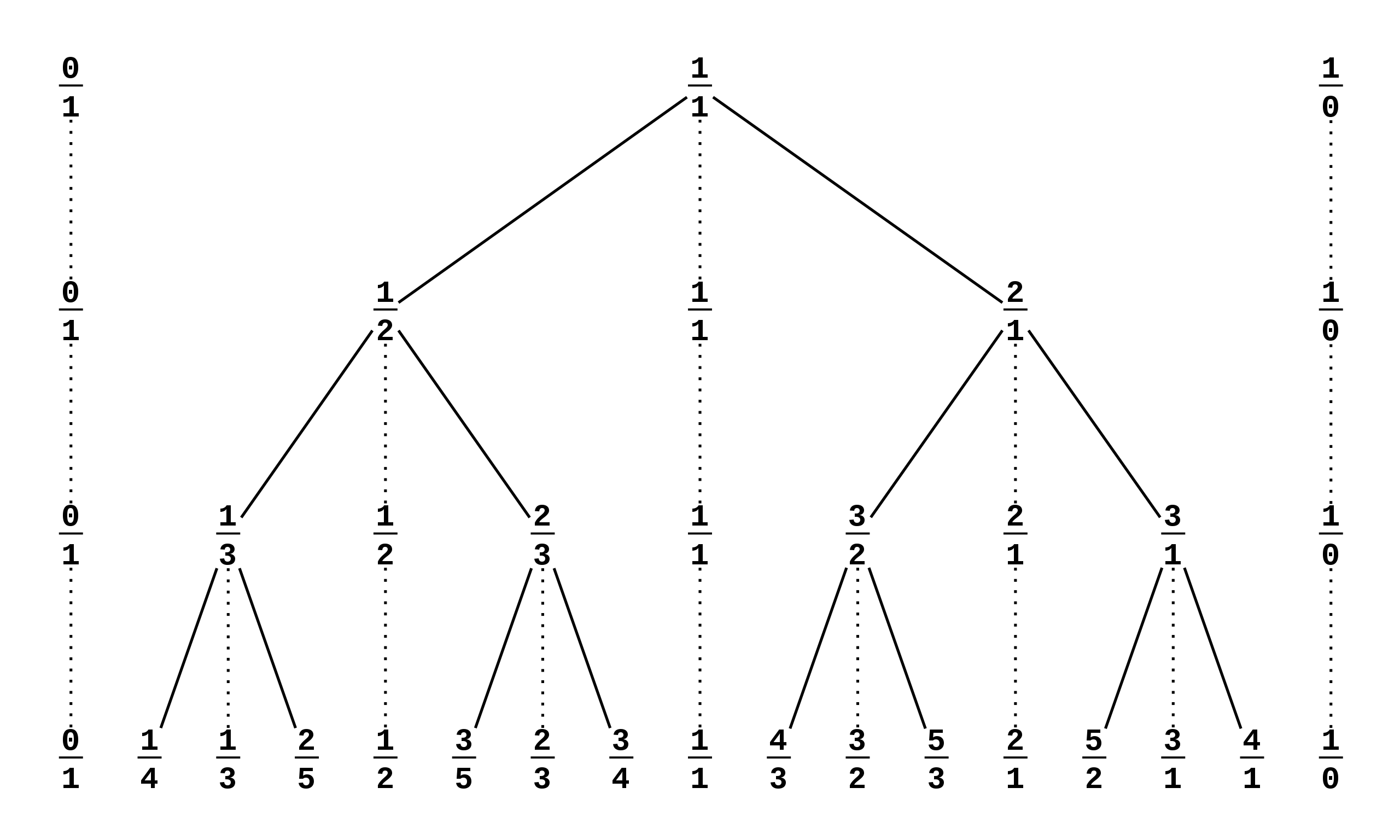
그림 1: Stern–Brocot Tree

확장된 페리 수열 $F' _1$부터 $F' _4$까지 활용하여 깊이 4의 Stern-Brocot Tree를 만들 수 있다.

이 트리는 (1) 완전 이진 검색 트리이며, (2) 모든 양의 유리수가 정확하게 한 번씩 등장한다는 강력한 성질을 가진다. 또한, 트리 그 자체로 유리수와 자연수 간의 일대일 대응을 잘 보여준다.

이러한 완전 이진 검색 트리를 Stern-Brocot Tree라고 부른다.

유리수 이분탐색

알고리즘 분야에서 Stern-Brocot Tree는 유리수를 대상으로 이분탐색을 할 수 있게 되었다는 점에서 그 의미가 깊다.

두 유리수 $ \displaystyle \frac{a}{b} < \frac{c}{d} $에 대하여, $\displaystyle \frac{a}{b}$ 초과 $\displaystyle \frac{c}{d}$ 미만의 모든 유리수를 담고 있는 Stern-Brocot Subtree의 루트 정점은 $\displaystyle \frac{a+c}{b+d}$이다.

이를 그대로 활용하면, 다음과 같은 이분탐색 알고리즘을 생각할 수 있다.

$ \displaystyle s := \frac{a}{b} = \frac{0}{1} $, $ \displaystyle e := \frac{c}{d} = \frac{1}{0} $으로 설정한다. 이제, 각 스텝마다 $s$ 초과 $e$ 미만인 유리수에 대하여 이분탐색을 수행한다.

중간값 $ \displaystyle m := \frac{ a+c }{ b+d } $을 잡자.

만약, $m$이 찾고자 하는 유리수라면, 탐색을 멈춘다.

아니라면, 찾고자 하는 유리수와 $m$에 대한 대소비교를 수행한다.

$(s, e)$를 $(s, m)$ 혹은 $(m, e)$로 대입한 후, 위의 과정을 반복한다.

이러한 이분탐색 과정을 통하여 최종적으로 기약분수 $ \displaystyle \frac{x}{y} $를 얻었다면, 탐색 횟수는 Stern-Brocot Tree에서 정점 $ \displaystyle \frac{x}{y} $의 깊이와 같으므로 $O(x+y)$이다.

과정 2.는 Stern-Brocot Tree의 정점에서 한 쪽 방향으로 내려가는 것을 나타낸다. 여기서, 연속으로 몇 번까지 같은 방향으로 내려가는지를 알아낼 수 있다면 탐색 횟수를 줄일 수 있다. 예를 들어, 중간값 $m$보다 작은 쪽으로 탐색을 이어나가야 한다면, $e$ 값을 $ \displaystyle \frac{ ta + c }{ tb + d } $ 꼴로 제한할 수 있다. 이것이 가능한 최대 정수 $t$를 이분탐색으로 찾으면, 전체 탐색 횟수를 $O(x+y)$에서 $O \left( x + \lg y \right)$로 크게 개선할 수 있다.

기하적 접근

다시 원래의 문제로 돌아오자. 우리는 아래의 그림과 같이 $ \displaystyle y = \frac{N}{x} $ 곡선 아래의 회색 영역에 존재하는 양의 정수 쌍 $(x, y)$의 수를 세어야 한다.

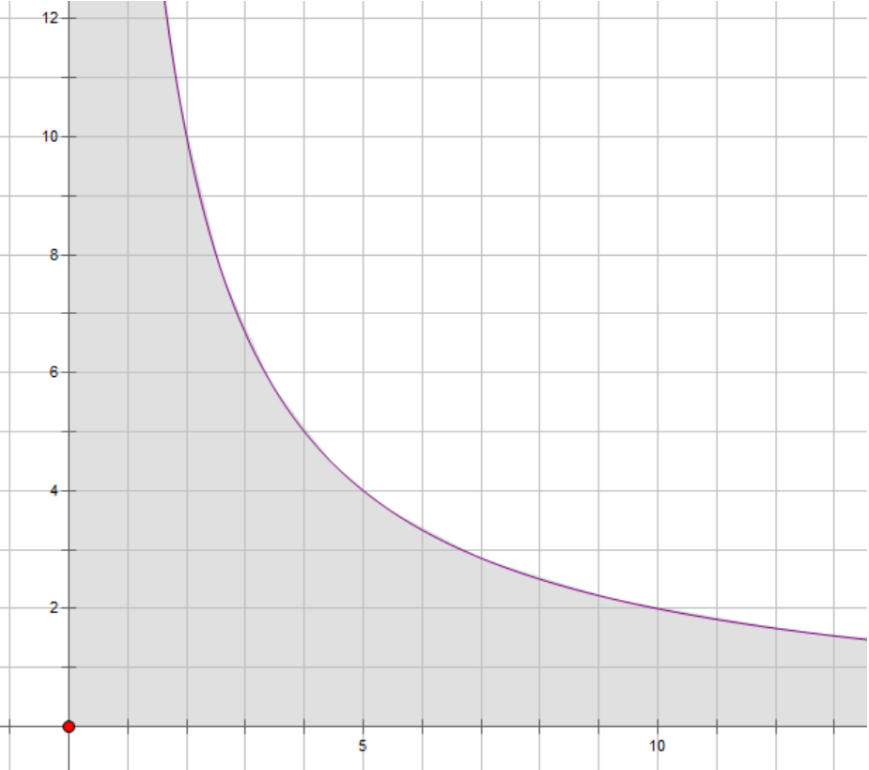
그림 2: $xy = 20$ 그래프와 회색 영역

$N = 20$이라면 위 회색 영역 내부의 정수 점의 개수를 세어야 한다.

이 그래프에서 기울기가 $-1$인 접선을 긋자. 아래의 그림에 접점 $G$, $x$ 축과 $y$ 축과의 교점 $P _x$, $P _y$을 나타내었다.

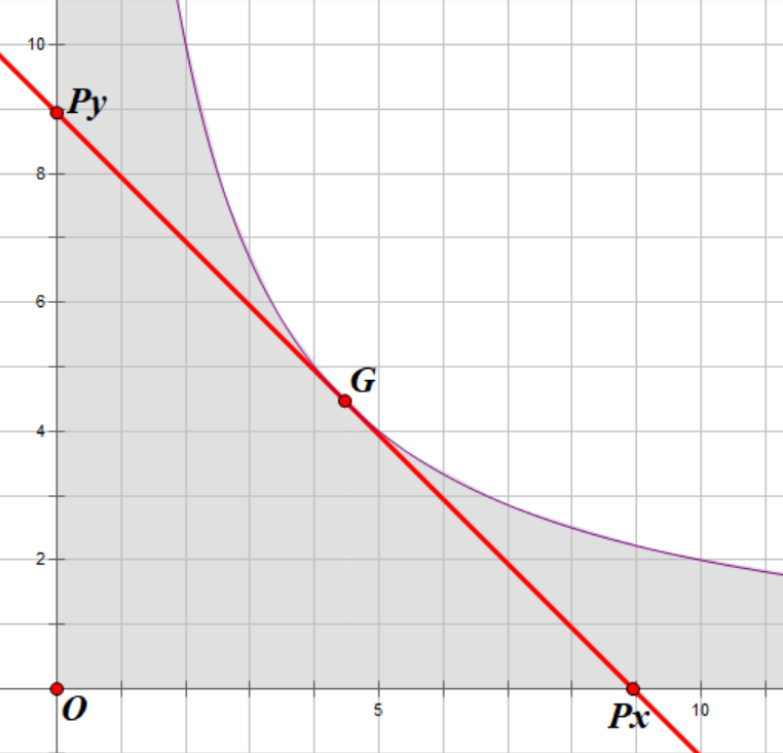
그림 3: $xy = 20$ 그래프와 기울기 $-1$의 접선

접점 $G$와 중요한 교점 두 개 $P _x$, $P _y$를 나타내었다. 접선 아래 영역의 정수 점의 개수는 쉽게 셀 수 있다.

여기서 아이디어는 이러하다. 곡선 아래의 정수 점의 개수를 세는 것은 어렵지만, 직선 아래의 정수 점의 수는 사칙연산을 이용하여 아주 쉽게 셀 수 있다.

우리는 남은 영역에 대하여 적당한 기울기의 접선을 그어 점의 개수를 세는 작업을 재귀적으로 반복하고자 한다. 정수 점의 개수는 유한하므로, 접선의 기울기를 잘 설정하였다면, 이러한 작업은 유한 시간 안에 종료할 것이다.

편의를 위하여, 그림 4와 같은 영역 내부의 정수 점의 개수를 $\displaystyle f \left( x _0, y _0, \frac{a}{b}, \frac{c}{d} \right)$로 나타내자. 이에 대한 엄밀한 정의는 다음과 같다.

음이 아닌 정수 $x _0$, $y _0$과 페리 이웃한 두 기약분수 $\displaystyle \frac{a}{b}$, $\displaystyle \frac{c}{d}$에 대하여,

점 $P \left( x _0, y _0 \right)$을 잡고

점 $P$로부터 각각 기울기 $\displaystyle - \frac{a}{b}$, $\displaystyle - \frac{c}{d}$의 접선을 그어 교점 $Q$, $R$를 잡았을 때

직선과 곡선으로 닫힌 삼각 영역 $PQR$ 내부의 정수 점의 개수를 $\displaystyle f \left( x _0, y _0, \frac{a}{b}, \frac{c}{d} \right)$로 정의한다.

인자가 상기한 조건을 만족하지 않으면, 편의상 $\displaystyle f \left( x _0, y _0, \frac{a}{b}, \frac{c}{d} \right) = 0$으로 정의한다.

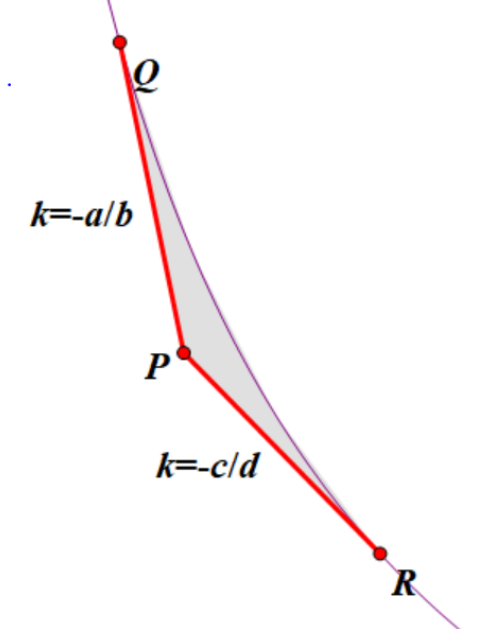
그림 4: 점 $P$, $Q$, $R$과 회색 삼각 영역

$\displaystyle f \left( x _0, y _0, \frac{a}{b}, \frac{c}{d} \right)$의 정의에서 사용되는 세 점을 나타내었다.

우리는 결국 $\displaystyle f \left( x _0, y _0, \frac{a}{b}, \frac{c}{d} \right)$가 0이 될 때까지 재귀적으로 탐색을 이어나가야 한다. 따라서, 이 함숫값을 계산할 수 있어야 한다. 이를 어떻게 계산할 수 있을까?

그림 4의 두 접선을 각각 새로운 축으로 잡고, 점 $P$를 원점으로 생각한 새로운 좌표계 $u-v$를 생각하자. $u$ 축이 직선 $PR$, $v$ 축이 직선 $PQ$이다. 이 경우 회색 영역은 다음과 같이 변환된다.

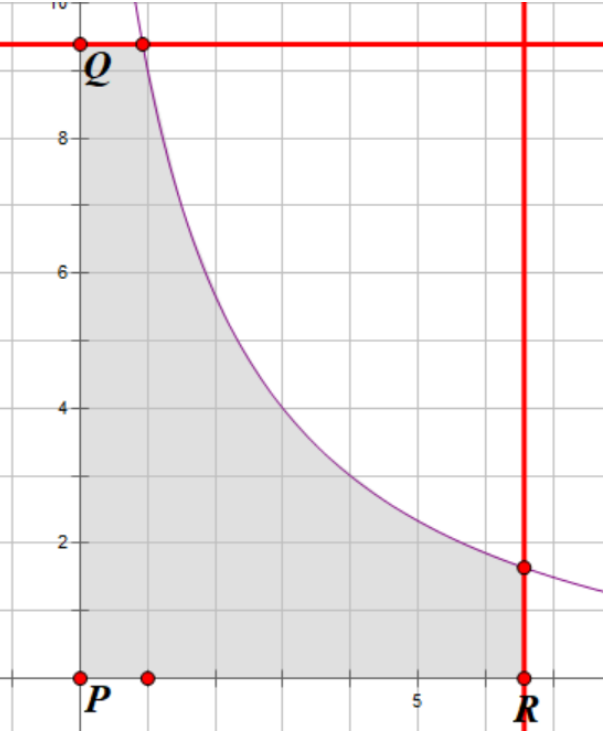
그림 5: 변환된 새로운 영역

드디어 우리는 재귀적으로 정수 점의 개수를 셀 수 있게 되었다!

시간 복잡도

재귀적으로 변하는 접선의 기울기는 Stern-Brocot Tree에서 경로를 따라 아래로 내려가는 것과 같으므로, 시간 복잡도를 아래와 같이 쓸 수 있다.

\[O \left( \sum _{ ad - bc = 1 } I \left[ \sqrt{ \frac{N}{ c/d } } - \sqrt{ \frac{N}{ a/b } } \ge b + d \right] \right)\] \[= O \left( \sum _{ ad - bc = 1 } I \left[ \frac{ \sqrt{bc + 1} - \sqrt{bc} }{ \sqrt{ac} } \ge \frac{ b + d }{ \sqrt{N} } \right] \right)\] \[= O \left( \sum _{ ad - bc = 1} I \left[ \frac{1}{ \sqrt{ab} c } \ge \frac{b+d}{\sqrt{N}} \right] \right) = O \left( \sum _{ad - bc = 1} I \left[ ab c^2 \left( b + d \right)^2 \ge N \right] \right)\]

마지막 줄에서는 $ \displaystyle \sqrt{x+1} - \sqrt{x} = O \left( \frac{1}{ \sqrt{x} } \right) $가 사용되었다.

이제, $t = bc$ 치환을 적용하면,

\[O \left( \sum _{t} \sum _{ b | t} \sum _{ a | (t+1) } I \left[ \frac{t^4}{ab} + t^3 + ab t^2 \ge N \right] \right)\] \[= O \left( \sum _{t = 1}^{N^{1/3}} \sigma(t) \sigma(t+1) \right) = O \left( \sum _{t=1}^{N^{1/3}} \sigma^2 (t) \right)\]

엄밀한 증명이나 식 전개는 생략하였다.

이제, 다음의 잘 알려진 정리를 적용하자.

\[\sum _{k=1}^{N} \sigma^2 (k) = \Theta \left( N \lg^3 N \right)\]

즉, 서술한 알고리즘의 시간 복잡도는 $ \displaystyle O \left( N^{ \frac{1}{3} } \lg^3 N \right) = \tilde{O}\left( N^{ \frac{1}{3} } \right) $ 임을 알 수 있다.

결론

수론적 함수는 정수론 뿐만 아니라 컴퓨터과학, 알고리즘, PS 분야에도 사용될 정도로 중요하며 그 폭이 아주 넓다.

우리는 대표적인 수론적 함수 $\sigma (n)$의 구간 합 $ \displaystyle \sum _{k=1}^{N} \sigma(k) $을 효율적으로 계산하는 알고리즘에 대하여 알아보았다.

일반적인 식 전개로는 $ \displaystyle O \left( \sqrt{N} \right) $까지 시간 복잡도를 줄일 수 있었다. 그러나, $N$이 아주 큰 수라면 이 방법도 아직은 느리다.

우리는 $ \displaystyle y = \frac{N}{x} $ 그래프와 구하고자 하는 값과의 관계를 알아내고, 그래프의 볼록성이라는 기하적 특성과 Stern-Brocot Tree 자료구조를 활용하여, 재귀적으로 값을 계산하는 새로운 알고리즘을 조사하였다.

또한, 이 알고리즘의 시간 복잡도가 $ \displaystyle \tilde{O} \left( N^{1/3} \right) $로 아주 효율적임을 밝혔다.

이러한 알고리즘의 아이디어는 다양한 볼록 함수에 대하여 접목시킬 수 있으며, 그 응용성이 높다. 다음 글에는 $\sigma (n)$ 외에 다른 수론적 함수의 구간 합을 효율적으로 계산하는 방법에 대하여 알아본다.