영 타블로의 조합론적 의미와 알고리즘적 응용 (1)

개요

영 타블로(Young tableaux)는 20세기 초반, 알프레드 영(Alfred Young)이 제안한 객체로, 조합론에서 군(Group)을 표현할 때 유용하게 사용할 수 있는 특수한 형태의 행렬이다.

본 글은 다소 어려운 개념인 영 타블로를 쉽게 서술하고, 조합론적인 의미를 설명하며, 이를 활용하여 얻을 수 있는 효율적인 알고리즘과 새로운 문제 해결 관점 등을 소개하고자 한다.

본문은 특별한 배경지식을 가지지 않아도 읽고 이해할 수 있도록 작성되었다.

용어의 정의

영 다이어그램

​ 영 타블로에 대하여 이야기하기 전에, 먼저 영 다이어그램(Young diagram)을 정의하자.

​ $\lambda = \left( \lambda _1, \lambda _2, \cdots, \lambda _k \right)$가 다음 조건을 모두 만족할 때, $\lambda$를 $N$의 자연수 분할이라고 하며, $\lambda \vdash N$이라고 표기하자.

• $\lambda _1, \lambda _2, \cdots, \lambda _k$는 모두 양의 정수
• $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _k > 0$
• $\displaystyle \sum _{i = 1}^{k} \lambda _i = N$

​ 양의 정수 $N$의 자연수 분할 $\lambda$가 주어지면, 우리는 “$\lambda$의 형태를 가지는 영 다이어그램”을 다음과 같이 정의할 수 있다.

$\lambda = \left( \lambda _1, \lambda _2, \cdots, \lambda _k \right)$의 형태를 가지는 영 다이어그램은

1. $k$개의 행으로 이루어진 표이며,
2. $i$번째 행의 길이는 $\lambda _i$이다$(1 \le i \le k)$.

영 다이어그램은 페러스 다이어그램(Ferrers diagram)이라고 부르기도 한다. 예를 들어, $(4, 2, 2, 1)$의 형태를 가지는 영 다이어그램은 아래의 그림과 같다.

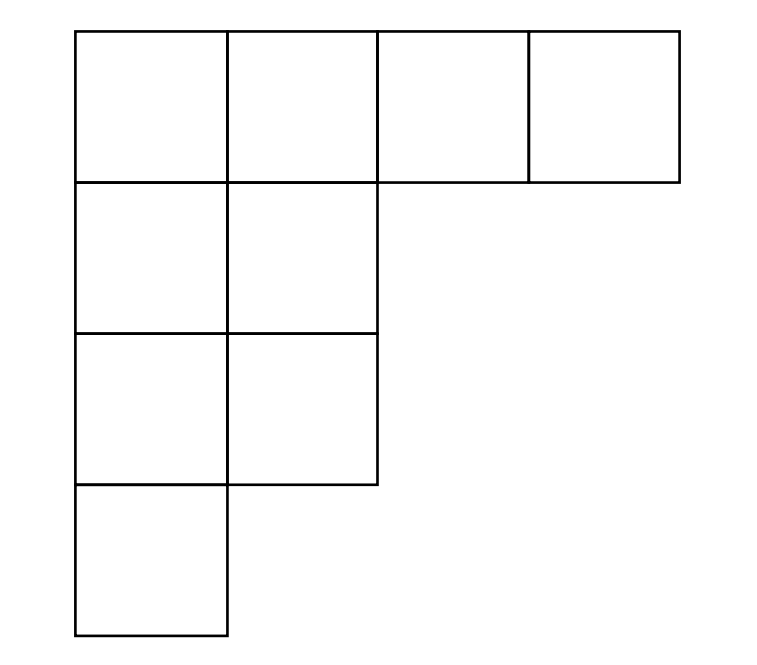
그림 1: $(4, 2, 2, 1)$ 형태의 영 다이어그램

영 타블로

​ 영 다이어그램의 각 칸에 양의 정수를 적자. 수를 어떻게 적냐에 따라서 표준 영 타블로(Standard Young tableaux) 혹은 준표준 영 타블로(Semistandard Young tableaux)를 정의할 수 있다.

1. $1$부터 $N$까지 서로 다른 양의 정수를 각 칸에 적고
2. 각 행에 대하여, 왼쪽에서 오른쪽으로 갈 수록 수가 증가하고
3. 각 열에 대하여, 위에서 아래로 갈 수록 수가 증가하면

이를 표준 영 타블로라고 부른다.

1. 각 행에 대하여, 왼쪽에서 오른쪽으로 갈 수록 수가 감소하지 않고
2. 각 열에 대하여, 위에서 아래로 갈 수록 수가 증가하면

이를 준표준 영 타블로라고 부른다.

그림 1에서 그림 2와 같이 수를 채웠다면, 이는 $(4, 2, 2, 1)$ 형태의 표준 영 타블로가 된다. 영 타블로에서 각 수가 등장하는 횟수를 기록한 벡터를 “영 타블로의 가중치”라고 부른다. 모든 표준 영 타블로의 가중치는 $(1, 1, \cdots, 1)$임이 자명하다. 표준 영 타블로에서 1번 조건은 필요에 따라 무시할 수 있다.

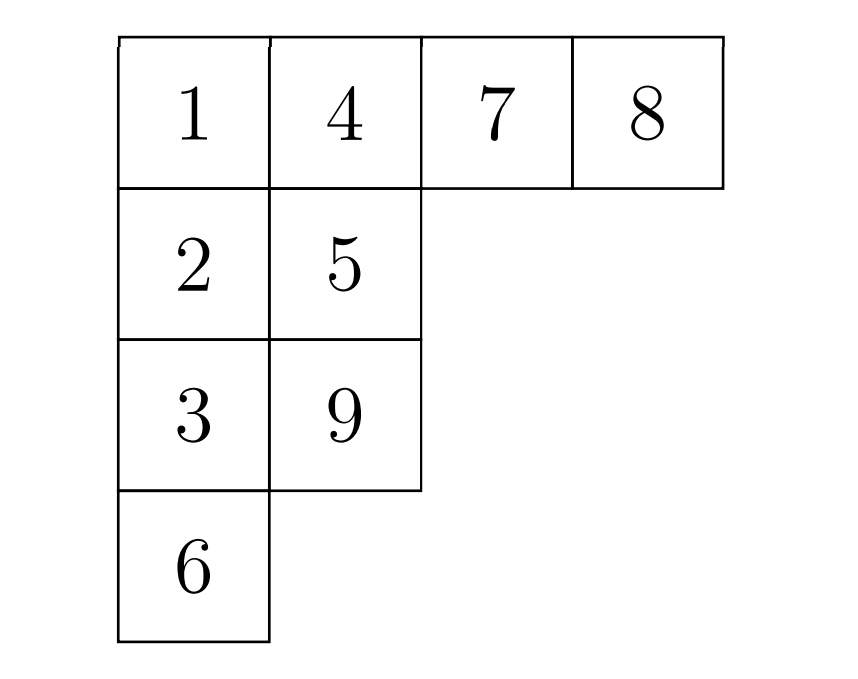
그림 2: $(4, 2, 2, 1)$ 형태의 표준 영 타블로

$(4, 2, 2, 1)$ 형태의 영 다이어그램에서 $1$부터 $9$까지 수를 조건에 맞게 칸에 채워 넣었음을 확인할 수 있다.

치우친 영 타블로

​ 이제, 두 개의 자연수 분할 $\lambda = \left( \lambda _1, \lambda _2, \cdots, \lambda _k \right)$과 $\mu = \left( \mu _1, \mu _2, \cdots, \mu _{k’} \right)$을 생각하자. 모든 $i$에 대하여, $\mu _i \le \lambda _i$가 성립하면, “$\lambda / \mu$ 형태의 치우친 영 타블로”를 정의할 수 있다.

$\lambda / \mu$ 형태의 치우친 영 타블로는

1. $i$번째 행이 $\lambda _i$개의 칸으로 이루어져 있으며
2. $i$번째 행 앞에 $\mu _i$개의 빈 칸이 있는

영 타블로를 의미한다.

예를 들어, $(9, 7, 5, 1) / (5, 3, 2)$ 형태의 치우친 표준 영 타블로는 아래와 같다.

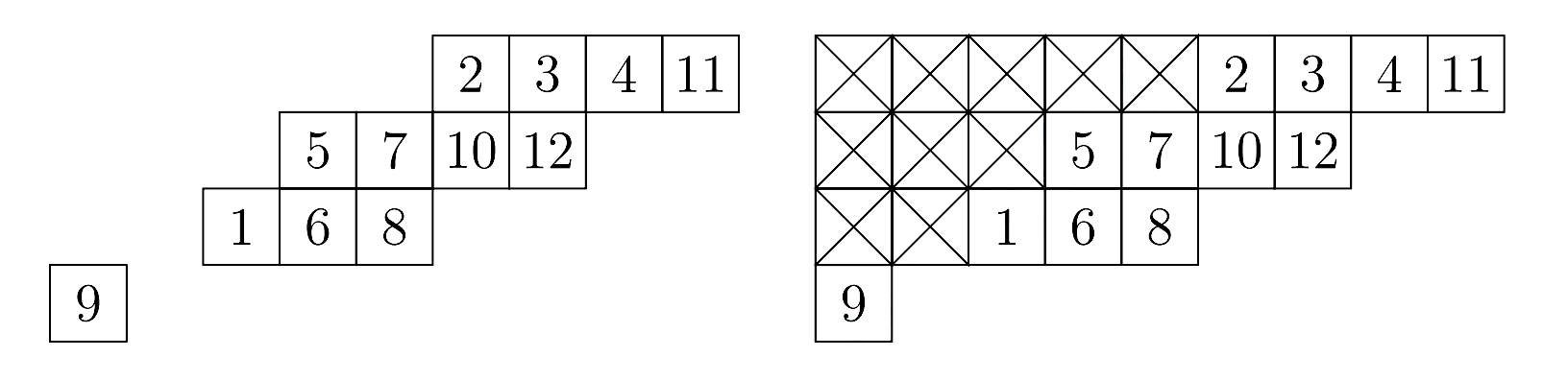
그림 3: $(9, 7, 5, 1) / (5, 3, 2)$ 형태의 치우친 표준 영 타블로

오른쪽 그림은 왼쪽 그림의 빈 칸을 명시적으로 표현한 것이다.

​ 이제, 영 타블로를 조합론적으로 어떻게 활용할 수 있는지 알아보자.

영 타블로의 조합론적 해석

​ 영 타블로는 순열 그 자체와, LIS와 같이 순열이 가지는 복잡한 특성 등을 시각적으로 이해할 수 있도록 도와준다. 대표적으로, Robinson–Schensted–Knuth correspondence는 표준 영 타블로와 순열을 대응하는 효과적인 방법을 제시한다.

​ RSK 대응 알고리즘에 대하여 알아보기 전에, 표준 영 타블로에 대한 몇 가지 중요한 연산을 정의하자.

행 삽입 연산

​ 먼저, 행 삽입 연산 $S \leftarrow x$를 정의하자.

표준 영 타블로 $S$와 양의 정수 $x$에 대하여, 행 삽입 연산 $S \leftarrow x$는 다음과 같이 정의된다.

1. 현재 확인하고 있는 행에 대하여, 그 행에서 $x$보다 큰 수 중에서 가장 작은 수를 $y$라고 하자. 처음에는 첫 번째 행부터 확인한다.
2. 만일, 그러한 $y$가 존재하지 않는다면, 그 행의 마지막에 $x$를 추가하고, 삽입 연산 작업을 종료한다.
3. 만약 그러한 $y$가 존재한다면, 수 $y$를 $x$로 바꾼다.
4. $x$의 값을 $y$로 설정한 후, 아래 행으로 넘어가서 과정 1.부터 다시 수행한다.

그림 4는 표준 영 타블로 $(2, 5, 9)(6, 7)(8)$에 수 $3$을 행 삽입하는 과정을 보여준다.

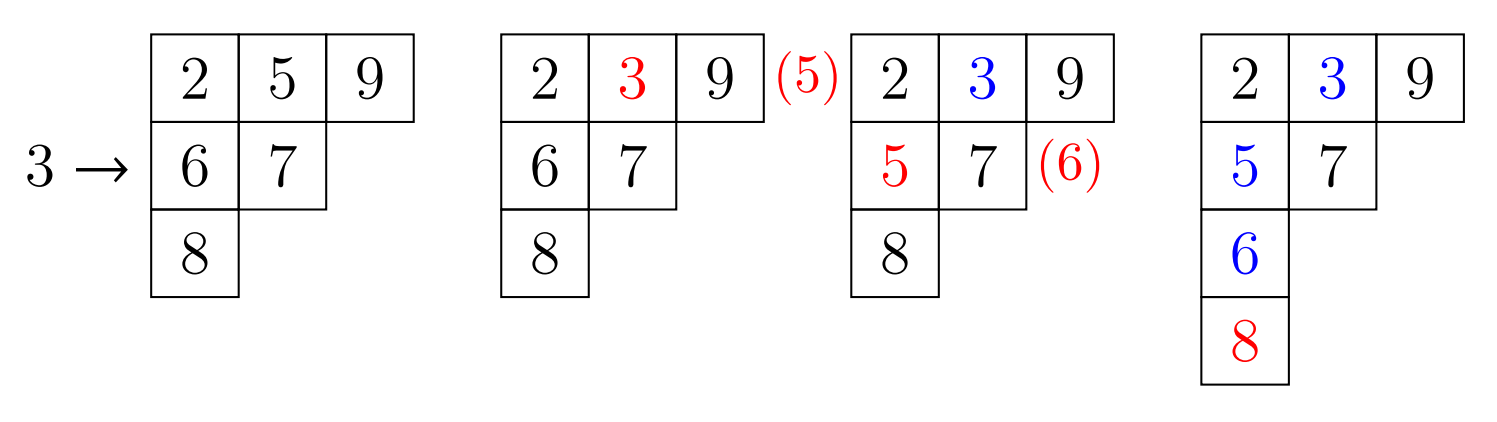
그림 4: $(2, 5, 9)(6, 7)(8) \leftarrow 3$ 연산 과정

중간 과정에서 괄호 안에 있는 빨간 수는 현재의 $x$ 값을 의미한다.

열 삽입 연산

​ 유사하게, 열 삽입 연산 $x \rightarrow S$ 또한 정의할 수 있다.

표준 영 타블로 $S$와 양의 정수 $x$에 대하여, 열 삽입 연산 $x \rightarrow S$는 다음과 같이 정의된다.

1. 현재 확인하고 있는 열에 대하여, 그 열에서 $x$보다 큰 수 중에서 가장 작은 수를 $y$라고 하자. 처음에는 첫 번째 열부터 확인한다.
2. 만일, 그러한 $y$가 존재하지 않는다면, 그 열의 마지막에 $x$를 추가하고, 삽입 연산 작업을 종료한다.
3. 만약 그러한 $y$가 존재한다면, 수 $y$를 $x$로 바꾼다.
4. $x$의 값을 $y$로 설정한 후, 오른쪽 열로 넘어가서 과정 1.부터 다시 수행한다.

그림 5는 표준 영 타블로 $(2, 5, 9)(6, 7)(8)$에 수 $3$을 열 삽입하는 과정을 보여준다.

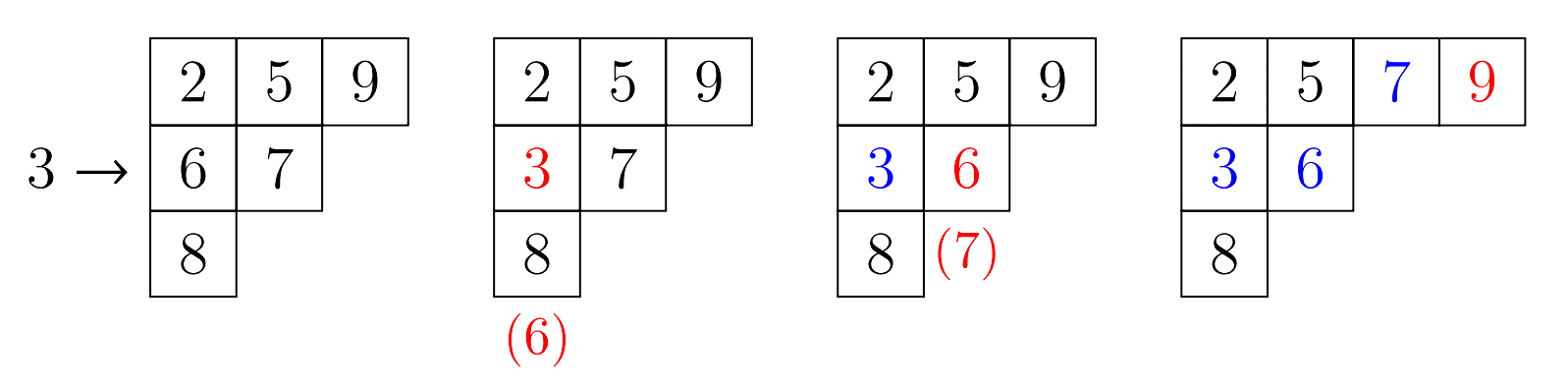
그림 5: $3 \rightarrow (2, 5, 9)(6, 7)(8)$ 연산 과정

​ 과연, 행 삽입 연산 혹은 열 삽입 연산 후에도 표준 영 타블로의 조건을 모두 만족할까? 아래의 정리는 우리의 궁금증에 대하여 긍정적인 답을 내놓는다.

삽입 연산의 정당성 정리

두 삽입 연산 $S \leftarrow x$와 $x \rightarrow S$의 결과는 모두 표준 영 타블로이다.

​ 행 삽입 연산 $S \leftarrow x$에 대해서만 살펴보자. 열 삽입 연산 $x \rightarrow S$는 행과 열의 역할을 바꾸어 동일하게 증명하면 된다.

과정을 반복함에 따라, $y$가 위치한 칸은 항상 아래로 진행하며, 오른쪽으로는 절대 진행하지 않는다. 따라서, 표준 영 타블로의 조건 2.와 3.을 만족한다.

마지막으로 살펴보아야 하는 점은, 아래의 행이 윗 행보다 길이가 길어지지 않는지 확인하는 것이다. 길이가 같은 인접한 두 행을 잡자. 앞에서 이야기 했듯이, $y$가 위치한 칸은 오른쪽으로 진행하지 않으므로, 윗 행에서 치환이 발생하였다면, 아래 행에서 조건을 만족하는 수 $y$를 반드시 찾을 수 있다. 즉, 아래 행에서 과정 2.가 진행되지 않으므로, 연산의 결과는 표준 영 타블로이다.

​ 즉, 두 삽입 연산은 잘 정의되어 있음을 알 수 있다.

삭제 연산

​ 마지막으로, 삭제 연산을 정의하자. 표준 영 타블로 $S$에서 칸 $(s, t)$를 삭제하는 연산은 다음과 같이 정의된다.

표준 영 타블로 $S$의 $s$번째 행, $t$번째 열의 칸 $(s, t)$에 적힌 수 $x := S_{s, t}$를 삭제하는 연산은 다음과 같다.

1. 만약 현재 확인하고 있는 행이 첫 번째 행이라면, $x$를 제거한 후, 삭제 연산 작업을 종료한다. 처음에는 $x$가 있는 행부터 확인한다.
2. 현재 확인하고 있는 행의 위쪽 행에 대하여, 그 행에서 $x$보다 작은 수 중에서 가장 큰 수를 $y$라고 하자.
3. 수 $y$를 $x$로 바꾼다.
4. $x$의 값을 $y$로 설정한 후, 윗 행으로 넘어가서 과정 1.부터 다시 수행한다.

이때, 칸 $(s, t)$는 모퉁이에 위치하여야 한다. 즉, 두 칸 $(s+1, t)$과 $(s, t+1)$가 존재하지 않아야 한다.

위 연산 작업의 과정 2.에서 $y$가 유일하게 존재함이 보장된다. 이는 표준 영 타블로의 정의를 이용하여 귀납법으로 증명할 수 있다. 아래의 그림은 표준 영 타블로 $(2, 3, 9)(5, 7)(6)(8)$에서 칸 $(4, 1)$을 삭제하는 연산 과정을 보여준다.

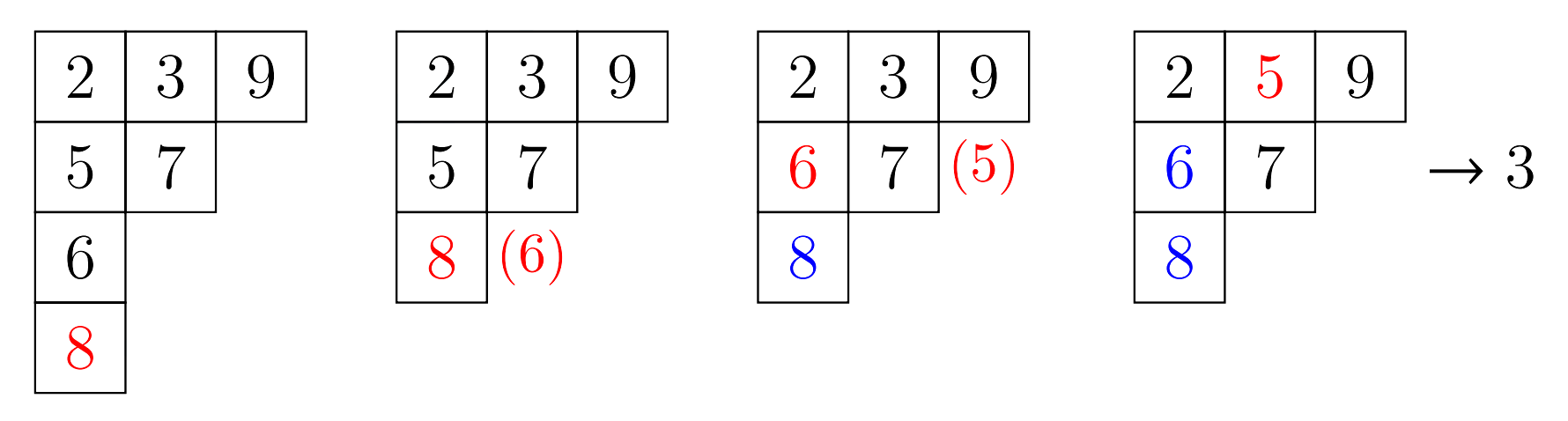
그림 6: $(2, 3, 9)(5, 7)(6)(8)$에서 칸 $(4, 1)$ 삭제 연산 과정

​ 당연하게도, 삭제 연산 후에도 표준 영 타블로의 모든 조건을 만족하는지 확인해야 한다. 예상했겠지만, 아래의 정리에 의하여 이는 옳다.

삭제 연산의 정당성 정리

삭제 연산의 결과는 표준 영 타블로이다.

​ 삭제하는 칸 $(s, t)$는 모퉁이에 위치함에 유의하자. 즉, 위에 있는 행이 아래에 있는 행보다 더 짧아지는 경우는 발생하지 않는다.

과정 2.에서 $y$의 정의에 따라, 각 행의 수가 증가하는 형태임은 자명하다.

과정 2.에서 $y$의 존재성 증명으로부터, 과정을 반복함에 따라, $y$가 위치한 칸은 항상 위로 진행하며, 절대로 왼쪽으로는 진행하지 않는다. 따라서, 삭제 연산의 결과를 볼 때, 각 열의 수 또한 증가하는 형태임을 알 수 있다. 즉, 삭제 연산의 결과는 표준 영 타블로이다.

​ 이렇듯, 위에서 제시한 세 개의 연산은 모두 잘 정의되어 있다.

이제, 연산을 자유롭게 사용하기 위하여 필요한, 아주 중요한 정리들을 소개한다.

역연산 정리

삭제 연산과 행 삽입 연산은 서로 역연산 관계이다.

즉, 표준 영 타블로 $S$에 행 삽입 연산을 하여 칸 $\left( s _1, t _1 \right), \left( s _2, t _2 \right), \cdots, \left( s _n, t _n \right)$을 생성하였다면, 칸 $\left( s _n, t _n \right), \left( s _{n-1}, t _{n-1} \right), \cdots, \left( s _1, t _1 \right)$에 대하여 순차적으로 삭제 연산을 적용하면 원래의 $S$를 얻을 수 있다.

​ $n=1$일 때만 보이면 충분하다. $n > 1$인 경우에는 $n$에 대한 귀납법으로 쉽게 증명할 수 있다.

$S \leftarrow x$ 연산을 하여, 칸 $(s, t)$가 생성되었다고 가정하자. 행 삽입 연산을 수행할 때, 각 과정에서 사용된 $x$ 값을 $x _1, x _2, \cdots, x _m$과 같이 나열하자. 즉, $x _1 = x$이며, $S \leftarrow x$ 연산의 결과를 볼 때, 칸 $(s, t)$에 적힌 값은 $x _m$이다.

여기서 칸 $(s, t)$에 대하여 삭제 연산을 수행하자. 귀납법을 적용하여, $i$번째 행에 삽입하는 수가 $x _i$와 동일하다고 가정하자. 적당한 $k$가 존재하여, $S _{i-1, k} < x _{i-1} < x _i < S _{i-1, k+2}$로 나타낼 수 있기에, $i-1$번째 행에서 삽입하는 수는 $x _{i-1}$가 되어야만 한다.

따라서, 삭제 연산의 과정은 정확하게 행 삽입 연산의 과정을 역순으로 나열한 것과 같다.

​ 이제, RSK 대응 알고리즘을 맞이할 준비를 모두 끝냈다.

RSK 대응 알고리즘

길이 $k$의 순열 $X = \left( x _1, x _2, \cdots, x _k \right)$에 대하여, $P _X$와 $Q _X$를 다음과 같의 정의하자.

• $P _X := \left( \left( \cdots \left( \left( x _1 \leftarrow x _2 \right) \leftarrow x _3 \right) \leftarrow \cdots \right) \leftarrow x _k \right)$
  • 즉, 반복적으로 수 $x _i$를 행 삽입한 표준 영 타블로.
• $Q _X$는 $P _X$와 동일한 형태의 영 다이어그램에 다음과 같은 규칙으로 수를 채워넣은 표이다.
  • $P _X$를 생성하는 과정에서, 수 $x _i$를 행 삽입할 때, 새롭게 생긴 칸을 $\left( s _i, t _i \right)$라고 하자.
  • $Q _X$의 칸 $\left( s _i, t _i \right)$의 값은 $i$로 정의한다.

행 삽입 연산의 정당성 증명을 통하여, $Q _X$가 표준 영 타블로임을 바로 확인할 수 있다.

​ 상당히 복잡하다. 예를 들어, 순열 $X = (1, 5, 3, 2, 6, 7, 4)$에 대하여 RSK 대응을 수행한 결과는 아래와 같다.

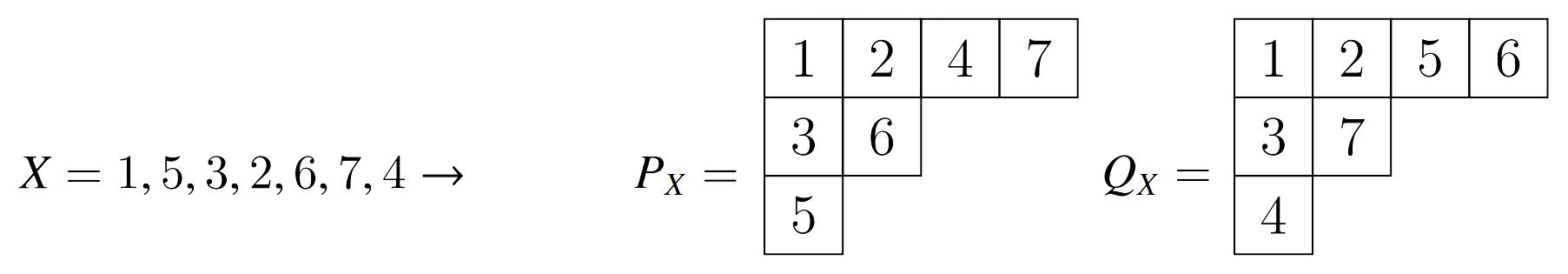
그림 7: 순열 $X = (1, 5, 3, 2, 6, 7, 4)$의 RSK 대응, $P _X$와 $Q _X$

$P _X$와 $Q _X$는 모두 조건 1.까지 만족하는 표준 영 타블로임을 알 수 있다.

​ 세 명의 천재 수학자 Robinson과 Schensted, Knuth에 따르면, 다음과 같은 강력한 조합적 관계가 성립한다고 한다.

RSK 대응 정리

길이 $N$의 순열과, 서로 같은 형태의 두 표준 영 타블로는 RSK 대응 알고리즘을 통하여 서로 일대일 대응된다.

​ 동일한 형태의 두 표준 영 타블로 $P$, $Q$가 주어졌을 때, $P _X = P$와 $Q _X = Q$를 만족하는 순열 $X = \left( x _1, x _2, \cdots, s _N \right)$를 찾을 수 있음을 보이면 된다.

$Q$에서 수 $i$가 적힌 칸을 $\left( s _i, t _i \right)$라고 하자. $i$를 $N$부터 $1$까지 차례대로 보면서, $P$에서 $\left( s _i, t _i \right)$에 대한 삭제 연산을 수행하였을 때 지워지는 수를 $x _i$로 정의하면 된다.

이렇게 얻어진 순열 $X$에 대하여, $X$와 $(P, Q)$가 서로 대응됨은 역연산 정리에 의하여 분명하다.

​ RSK 대응 정리에 따라, 다음 따름정리를 얻는다.

RSK 따름정리

$\lambda$ 형태의 표준 영 타블로의 개수를 $t _\lambda$라고 하자. 양의 정수 $N$에 대하여 다음이 성립한다.

\[\sum _{ \lambda \vdash N } \left( t _\lambda \right)^2 = N!\]

​ 우리는 자연수 분할과 표준 영 타블로의 가짓수, 순열에 관한 중요한 항등식을 얻었다.

이를 조합론적으로 어떻게 활용할 수 있는지는 다음 포스트에 이어서 설명한다.

​

결론

​ 영 타블로와 세 가지 연산의 정의를 살펴보고, 역연산 정리 등 아주 중요한 정리를 제시하였다

조합론적으로 중요한 의미를 지닌 RSK 대응 알고리즘에 대하여 알아보았으며, 이 알고리즘은 순열과 표준 영 타블로 쌍을 일대일 대응시킴을 RSK 대응 정리를 통하여 증명하였다. 이로부터, 영 타블로의 가짓수에 대한 중요한 항등식을 얻을 수 있었다.

​ 다음 포스트에는 RSK 대응 정리를 대칭 행렬과 같은 특수 군에 적용하여 영 타블로의 새로운 성질을 조사하고, 이를 통하여 순열의 LIS 등에 관한 새로운 접근 방법을 소개한다.